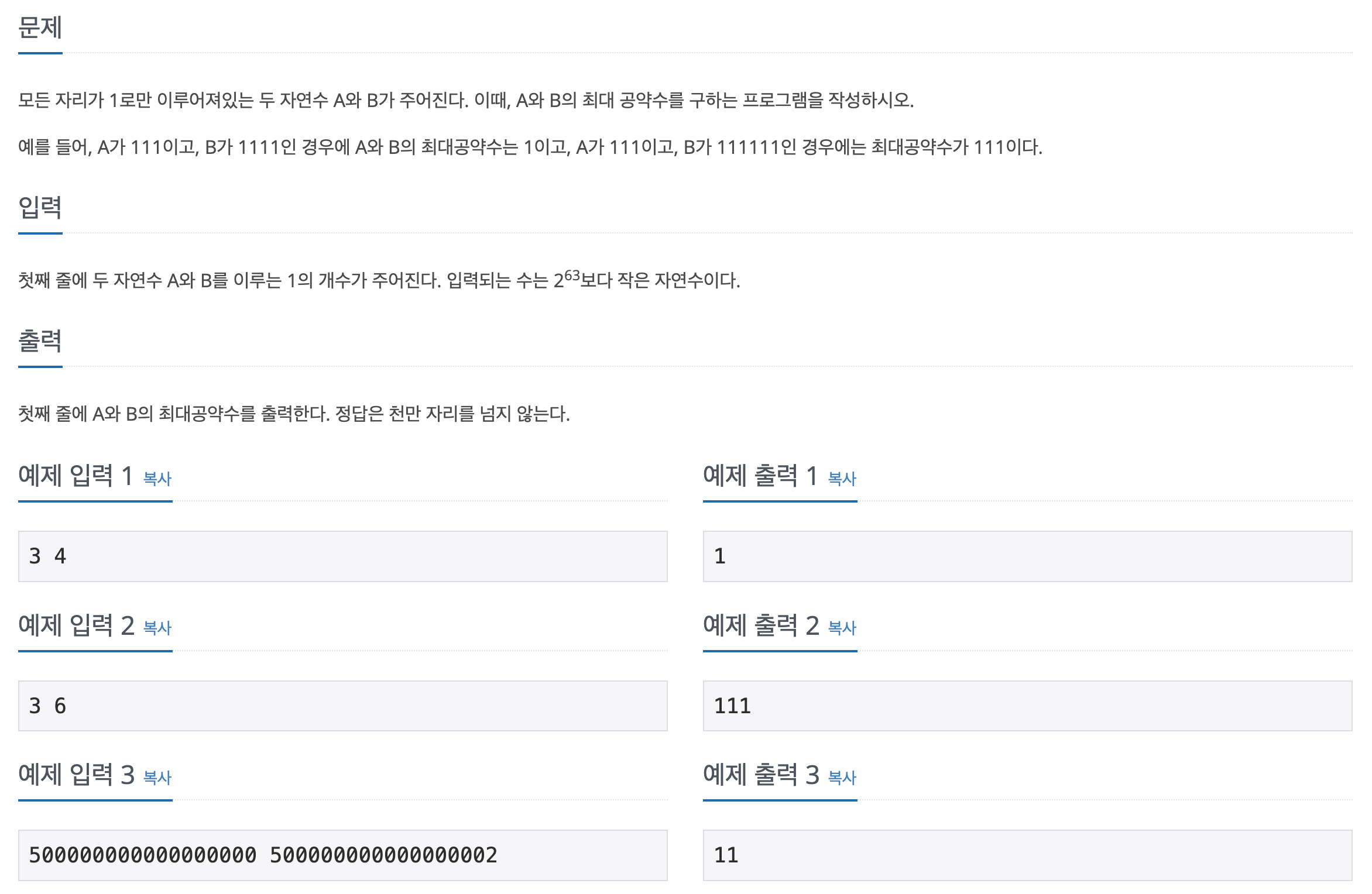
📌 문제
📌 풀이
처음에는 입력값이 실제 정수가 아닌 1의 개수라서 이를 정수로 변환하는 함수를 만들었다. 하지만 그렇게 하면 입력값이 클 경우 시간이 너무 오래 걸리는 경우가 생겼다.
몇 번 실제로 값을 계속 넣어 보니 겉으로만 1의 개수이지, 1의 개수들끼리 최대공약수를 구하여 이를 정수로 변환만 하면 된다.
이를 눈치채지 못하면 계속 돌고 돌아 멘붕에 빠질 수 있다.
최대공약수를 구하는데 사용한 유클리드 호제법(Euclidean Algorithm)은 아래의 링크에서 자세히 설명해 두었다.
[재귀] 유클리드 호제법과 최대공약수, 최소공배수
유클리드 호제법을 배워 보고 재귀적으로(recursively) 구현한 것과 반복적으로(iteratively) 구현한 것을 서로 비교해 보자. [알고리즘] 재귀(Recursion)에 대한 개념은 아래 링크 참고 [알고리즘] 재귀(Rec
andy-archive.tistory.com
📌 코드
// 입력 값을 Int의 배열로 할당
let arr = readLine()!.split(separator: " ").map{ Int(String($0))!}
// A, B 할당
var A: Int = arr[0]
var B: Int = arr[1]
// 반복문에 쓰일 범위를 두 수의 최대공약수로 할당
var range: Int = gcd(A, B)
// 결괏값 초기화
var result: String = ""
// 최대공약수만큼 문자열 "1"을 계속 추가
while (range > 0) {
result += "1"
range -= 1
}
// 결괏값 출력
print(result)
// 재귀적으로 최대공약수를 구하는 함수 정의
func gcd(_ a: Int, _ b: Int) -> Int {
let m: Int = max(a, b)
let n: Int = min(a, b)
if n == 0 {
return m
}
else {
return gcd(n, m % n)
}
}'코딩 테스트 > 백준' 카테고리의 다른 글
| [백준] (Swift) 10815번: 숫자 카드 (0) | 2023.04.11 |
|---|---|
| [백준] (Swift) 2981번: 검문 (0) | 2023.04.07 |
| [백준] (Python/Swift) 3040번: 백설 공주와 일곱 난쟁이 (0) | 2023.03.25 |
| [백준] (Swift) 1157번: 단어 공부 (0) | 2023.03.22 |
| [백준] (Swift) 3613번: Java vs C++ (0) | 2023.03.21 |




댓글