지난 글에 분할 정복 알고리즘의 개념에 대해 알아 보았다. 이제는 실제로 이를 적용한 합병 정렬에 대해 알아 보자.
[알고리즘] 분할 정복(Divide and Conquer) 개요
정렬 알고리즘에서 버블 정렬과 선택 정렬, 삽입 정렬에 대해 알아 보았다 이 세 가지 정렬 알고리즘은 코드가 직관적이긴 하지만 $n$(데이터의 크기)에 대한 이중 for 문으로 되어 있기에 굉장히
andy-archive.tistory.com
📌 정의
합병 정렬(merge sort)은 주어진 배열을 더 이상 쪼갤 수 없을 때까지 재귀적으로 데이터 크기의 절반으로 계속 나누고, 다시 정렬을 통합하여 정렬하는 알고리즘이다.
📌 동작 과정
합병 정렬은 요소가 하나가 될 때까지 계속해서 절반으로 나눈 뒤, 조합해 가면서 정렬해 나간다. 이를 재귀적으로 구현하는 것이 핵심이다.
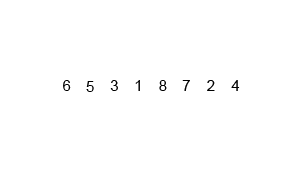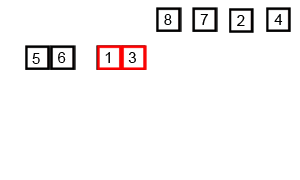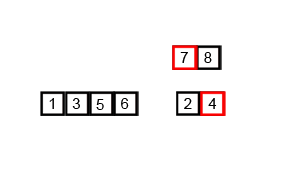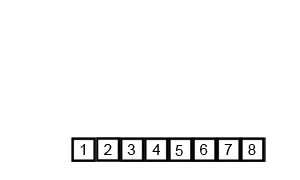
주어진 정렬은 검은색 박스로 점점 절반씩 나누어진다. 하나까지 쪼개진 요소들은 하나씩 조합해가면서 정렬을 완성해 나간다.
1. 분할(Divide)
- 주어진 배열을 데이터 크기 $N$ 의 절반 $\frac{N}{2}$ 으로 나누어 2개의 부분 배열로 분할한다.
- 이를 더 이상 쪼갤 수 없을 때까지(데이터 크기 1~2개의 부분 배열) 분할한다.
2. 정복(Conquer)
- 나누어진 부분 배열에 대해서 재귀적으로 합병 정렬을 한다.
- 단, 데이터 개수가 1개인 부분 배열은 이미 정렬된 상태로 간주한다.
3. 조합(Combine)
- 정렬한 2개의 부분 배열을 통합하여 원래 크기의 정렬된 배열로 만든다.
📌 코드 1
# 재귀를 이용한 합병 정렬 함수 정의
def merge_sort(arr):
# 종료 조건은 배열의 길이가 0 또는 1일 때
if len(arr) <= 1:
return arr
# 절반으로 나누어 왼쪽 배열과 오른쪽 배열로 분할
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]
# 아까 나눈 왼쪽 배열과 오른쪽 배열을 각각 다시 호출
left_half = merge_sort(left_half)
right_half = merge_sort(right_half)
# 왼쪽 배열과 오른쪽 배열을 합병한 것을 반환
return merge(left_half, right_half)
# 합병 함수 정의
def merge(left_half, right_half):
# 반환할 배열과 왼쪽 절반과 오른쪽 절반에 대한 인덱스 초기화
result = []
i = j = 0
# 왼쪽 절반이나 오른쪽 절반 중 인덱스가 초과할 때까지 반복
while i < len(left_half) and j < len(right_half):
if left_half[i] < right_half[j]:
result.append(left_half[i])
i += 1
else:
result.append(right_half[j])
j += 1
# 위의 루프에서 초과했을 경우 남은 부분 배열을 모두 더함
result += left_half[i:]
result += right_half[j:]
# 정렬된 배열 반환
return result
# 테스트 코드
if __name__ == "__main__":
array = [6, 5, 3, 1, 8, 7, 2, 4]
print(array)
print(merge_sort(array))[6, 5, 3, 1, 8, 7, 2, 4]
[1, 2, 3, 4, 5, 6, 7, 8]
📌 코드 2
def merge(arr, low, high):
temp = []
mid = (low + high) // 2
i, j = low, mid + 1
while i <= mid and j <= high:
if arr[i] <= arr[j]:
temp.append(arr[i])
i += 1
else:
temp.append(arr[j])
j += 1
while i <= mid:
temp.append(arr[i])
i += 1
while j <= high:
temp.append(arr[j])
j += 1
for k in range(low, high + 1):
arr[k] = temp[k - low]
return arr
def merge_sort(arr, low, high):
if (low >= high):
return # base case
mid = (low + high) // 2
merge_sort(arr, low, mid)
merge_sort(arr, mid+1, high)
sorted_array = merge(arr, low, high)
return sorted_array
# test code
if __name__ == "__main__":
unsorted_array = [5, 6, 4, 0, 2, 1, 7, 3, 8]
print(f"unsorted array :\t {unsorted_array}")
print(f"sorted array :\t\t {merge_sort(unsorted_array, 0, 8)}")unsorted array : [5, 6, 4, 0, 2, 1, 7, 3, 8]
sorted array : [0, 1, 2, 3, 4, 5, 6, 7, 8]
'알고리즘 > 분할 정복' 카테고리의 다른 글
| 퀵 정렬(Quick Sort) in Python (0) | 2023.04.04 |
|---|---|
| 분할 정복 알고리즘(Divide and Conquer Algorithm) (0) | 2023.03.29 |


댓글