퀵 정렬(Quick Sort) in Python

목차

머리말

들어가기 전에

합병 정렬에 이어 분할 정복 알고리즘을 이용한 두 번째 정렬인 퀵 정렬에 대해 알아 보자.

퀵 정렬(Quick Sort)

정의

기준 데이터(피벗, pivot)를 설정하여, 그 기준보다 큰 데이터와 작은 데이터를 구분하는 '분할(partition) 알고리즘'을 재귀적으로(recursively) 반복하여 다시 조합해 나가는 정렬 알고리즘

배열 중에서 임의의 데이터를 '피벗(pivot)'이라 불리는 기준 데이터로 설정한다. 피벗을 기준으로 자기보다 크기가 작은 그룹과 큰 그룹을 최대한 분할한 이후 조합하면서 정렬을 해 나가는 알고리즘이다.

동작 과정

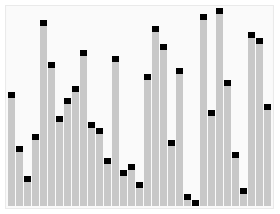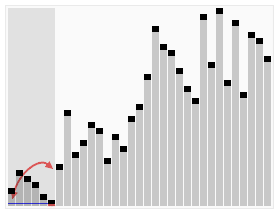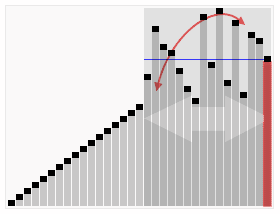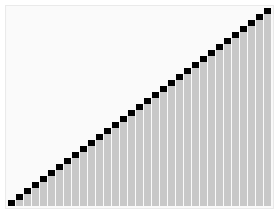
Sorting quicksort animation - Quicksort - Wikipedia

동작 과정

분할 정복 알고리즘에 맞게 세 단계로 나누어 설명하면 아래와 같다.

(1) 분할 (Divide → Partition)

퀵 정렬에서는 분할을 divide가 아닌 partition이라 한다.

분할 방법에 따라 여러 변형이 존재하는데, 여기서는 두 기법(로무토, 호어)에 대해 다룰 것이다.

(1)-1. 로무토(Lomuto) 기법

피벗이 맨 오른쪽에 위치하며, 비교할 두 인덱스 i와 j가 모두 왼쪽에 위치하여 점차 오른쪽으로 이동한다.

1. i와 j를 맨 왼쪽에서부터 시작, 피벗은 맨 오른쪽에 위치
2. j를 증가시키면서j의 요소 값이 피벗보다 작을 경우, swap(A[i], A[j])
3. i += 1
4. j가 맨 오른쪽에 도달하면, 피벗과 i의 요소 값을 swap

(1)-2. 호어(Hoare) 기법

피벗이 맨 왼쪽에 위치하며  비교할 두 인덱스 i는 맨 왼쪽, j는 피벗의 왼쪽에 위치하여 두 인덱스가 점차 가운데로 이동한다.

1. i는 (맨 왼쪽 + 1)에서, j는 맨 오른쪽에서 시작. 피벗은 맨 왼쪽에 위치
2. i에서부터는 피벗보다 큰 값을, j에서부터는 피벗보다 작은 값을 선택하여 두 값을 swap.
3. 위를 반복하여 큰 값과 작은 값의 위치가 서로 엇갈리는 경우 피벗과 작은 값을 swap.

(2) 정복(Conquer)

• 피벗을 중심으로 나뉜 두 그룹을 재귀적으로(recursively) 퀵 정렬 수행.

(3) 조합(Combine)

• 따로 필요하지 않음.

특징

• Tony Hoare가 최초로 개발하였으며(1959), 분할 방법에 따라 여러 변형이 존재한다.
  • 가장 많이 사용되는 기법은 두 가지(by Tony Hoare or Nico Lomuto)이다.
• 합병 정렬(merge sort)과 같이 가장 효율적인 정렬 알고리즘이다.
  • 수많은 프로그래밍 언어에서 정렬 라이브러리로 사용된다.
• 시간복잡도
  • $O(N\log N)$ --> 평균
  • $O(N^2)$ --> 이미 정렬된 데이터에 대해서 최악의 경우가 발생

실습

in Python

# 분할 함수 정의 (by Lomuto)
def partition(A, low, high):
    pivot_idx = low  # 피벗의 인덱스를 임의의 값으로 설정 (현재는 제일 왼쪽 값으로 설정)
    pivot = A[pivot_idx]

    A[pivot_idx], A[high] = A[high], A[pivot_idx]  # 비교를 위해 피벗을 가장 오른쪽 값과 swap

    i = low
    for j in range(low, high):
        if A[j] < pivot:  # 인덱스 j는 피벗보다 작은 값을 찾아서, A[i]와 swap
            A[i], A[j] = A[j], A[i]
            i += 1

    pivot_idx = i  # 반복문을 마친 배열에서 i는 피벗의 인덱스가 되어야 함.
    A[pivot_idx], A[high] = A[high], A[pivot_idx]

    return pivot_idx


# 퀵 정렬 함수 정의
def quick_sort(A, low, high):
    if low < high:
        pivot_idx = partition(A, low, high)  # 분할 함수를 진행하여 피벗을 기준으로 분할을 진행
        quick_sort(A, low, pivot_idx - 1)  # 분할의 왼쪽 부분에 대해서 재귀
        quick_sort(A, pivot_idx + 1, high)  # 분할의 오른쪽에 대해서 재귀

# 테스트 코드
if __name__ == "__main__":
    A = [5, 6, 4, 0, 2, 1, 7, 9, 3, 8]
    low, high = 0, len(A)-1

    print(f"BEFORE QUICK_SORT : {A}")
    quick_sort(A, low, high)
    print(f"AFTER QUICK_SORT  : {A}")

BEFORE QUICK_SORT : [5, 6, 4, 0, 2, 1, 7, 9, 3, 8]
AFTER QUICK_SORT  : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

분할 함수(partition)의 진행 과정

""" 테스트 코드의 분할 함수 재현

| == pivot
* == swap

5 6 4 0 2 1 7 9 3 8   swap(A[pivot_idx], A[high])
|*                *

8 6 4 0 2 1 7 9 3 5   swap(A[i], A[j])
*   *             |
i
j j j*

4 6 8 0 2 1 7 9 3 5   swap(A[i], A[j])
  *   *           |
  i
    j j*

4 0 8 6 2 1 7 9 3 5   swap(A[i], A[j])
    *   *         |
    i
        j*

4 0 2 6 8 1 7 9 3 5   swap(A[i], A[j])
      *   *       |
      i
          j*

4 0 2 1 8 6 7 9 3 5   swap(A[i], A[j])
        *       * |
        i
            j j j*

4 0 2 1 3 6 7 9 8 5   swap(A[pivot_idx], A[high])
          *       |*

4 0 2 1 3 5 7 9 8 6   분할 함수 종료 -> 피벗의 인덱스 값 반환
          |
(small)   |  (big)

- 위와 같이 분할(partition) 함수에 의해 5를 기준으로 분할 완료.
- 이것을 재귀로 반복하면 퀵 정렬이 완성
"""

꼬리말

참고 자료

• 챕터5-3. 정렬 | 퀵 정렬(Quick Sort) - Hoare(호어) / Lomuto(로무토) 분할 알고리즘

 

수정일: 2023-12-27 (수)